Posted on February 17, 2021 by Lisa Ward
by Henry S. Pettingill, Marc Bond, Jeff Brown, Peter Carragher, Mark Golborne, Jim Gouveia, and Bob Otis
One of the common questions that teams ask us when reviewing subsurface projects is, “How should we set our input ranges for volumetrics?” This article introduces a new series that will address that question.
STATEMENT OF THE PROBLEM
Many published works over the years have documented the importance of predicting what we find for our oil and gas portfolios, in both the exploration and development phases of the project life cycle. While it is impossible to repeatedly find exactly ‘the number’ for every prospect, well, or development, it is possible to get close the prediction on a portfolio basis. The fundamental concept is that for both prospects and portfolios, we can state our prediction in ranges, and additionally in terms of measures of central tendency (our ‘expectation’, commonly the arithmetic mean) and dispersion around that central tendency. The consequence of this latter statement is that we are able to give leadership ‘one number’ for an expectation – which is usually what both the executive suite and the investment community want from us.
So why do we use ranges? Simply put, it has been repeatedly shown that our predictions are better in the long run if, instead of using single values for each input parameter, we employ ranges to ultimately derive confidence intervals and a single value of our ‘expectation’ for that parameter (e.g. Pettingill, 2005). It also makes the elimination of systematic estimating bias more effective, as statistically rigorous post-mortem analyses become possible.
HISTORY OF EMPLOYING PROBABILISTIC RANGES FOR PREDICTIONS
As far as we can tell, the pharmaceutical industry led the way in the 1920s by employing ranges in probabilistic predictions. The first employment of these methods in oil and gas volume prediction was documented in the late 1960s (for instance, Newendorp, 1968).
While most of the major upstream petroleum companies were employing these methods, they advanced and gained wider usage following seminal publications in the 1970s and 1980s by Ed Capen, Pete Rose, Bob Megill, Paul Newendorp, and others (see references below). These references have withstood the test of time and remain relevant today, so we highly recommend reading them.
Later works validated the concepts by demonstrating that pre-drill predictions as a whole were improved with the implementation of probabilistic ranges. These are well documented by Otis and Schneidermann (1997), Johns (1998), Ofstad et al. (2000), McMaster and Carragher (2003) and Pettingill (2005).
Fast forwarding to 2021, what have we observed over the years with respect to the application of these concepts? First, there are still many questions that arise on the topic from the upstream community. Second, some of the digital-era staff have not received an in-depth education on the fundamental concepts that drive input ranges. And finally, it seems like many of us who learned these methods have forgotten some of the fundamentals (or at least become rusty!).
HOW DO WE ADDRESS THE ISSUE OF SETTING RANGES FOR VOLUMETRICS?
Three fundamental concepts define the modern concepts for pre-drill volumetric assessment: 1) the jump from single deterministic input parameters to probabilistic inputs, 2) the use of continuous probability distributions (e.g., normal, lognormal), and 3) employing confidence intervals associated with these input distributions, and as a consequence, the final output distribution of recoverable resources.
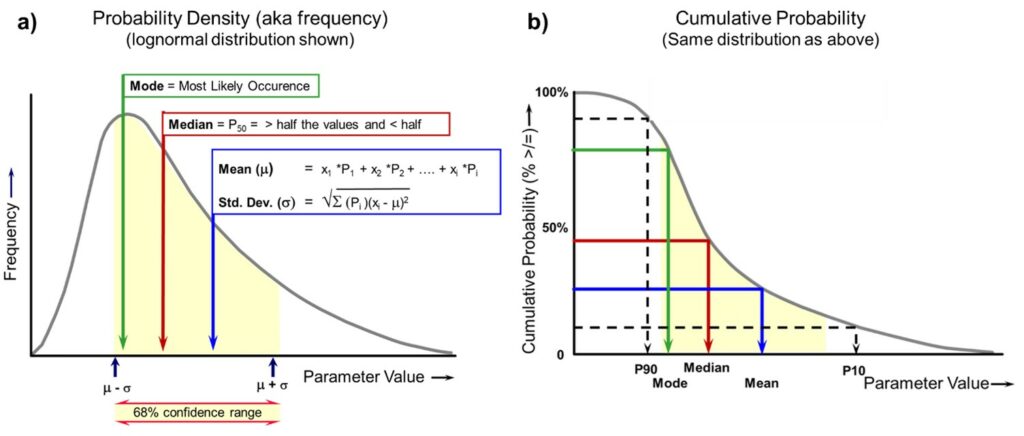
These probabilistic ranges can be characterized by parameters such as probability percentiles (P10, P90, etc.), mean, variance or standard deviation, and P10:P90 ratios (Figure 1). We will expound on these in a future blog. [note: in this blog, we define P10 as high and P90 as low]. The biggest benefit from using these probabilistic ranges is the ability to state our predictions in terms of confidence, e.g. “I have a 90% chance of finding __ mmboe or greater, a 50% chance of getting __ mmboe or greater, and a 10% chance of getting __ mmboe or greater”. Another great advantage is the ability to characterize the distribution with a single mean value or the expectation that encompasses the entire output distribution: the mean, which is the average outcome. This allows us not only to understand the anticipated value of our portfolio as if we drilled our prospect thousands of times but also allows us to objectively compare and rank projects within a portfolio.
Figure 1. Probability graphs (lognormal distribution shown): a) probability density graph, b) cumulative probability graph. Note that we are using the “greater than or equal to” convention, with P90 as the low-end percentile. The concept applies to both the input parameter as well as the output distribution.
FURTHER TOPICS IN THIS SERIES
This series will evolve as we go along, so a precise schedule of topics is not set (of course, that will be driven largely by the comments from our readers!). Future topics being contemplated are:
— What should our modeled ranges represent?
— Different approaches to assessing uncertainty in Net Rock Volume (NRV)
— How to handle input parameters that use Averages (net pay, Phi, Sw, etc.)
— How to select ranges in the prospect area
— Spatial Concepts: how to jump from a map to a volumetric input distribution
— Direct Hydrocarbon Indicators (DHIs): specific considerations when choosing volumetric inputs
— Important statistical concepts: Mean, Variance, Standard Deviation, and P10/P90 ratios
ACKNOWLEDGEMENTS
We wish to thank all the authors of the works cited here, as well as the countless others not cited, for their contributions to this topic and our industry. They are the true heroes of this journey of learning. We also extend our gratitude to our colleagues at Rose and Associates.
FURTHER READING
— Capen, E. C. (1976), The difficulty of assessing uncertainty, Journal of Petroleum Technology, August 1976, pp. 843-850.
— Carragher, P. D. (1995), Exploration Decisions and the Learning Organization, Society of Exploration Geophysicists, August 1995, Rio de Janeiro.
— Johns, D. R., Squire, S. G., and Ryan, M. G. (1998), Measuring exploration performance and improving exploration predictions—with examples from Santos’ exploration program 1993-96, APPEA Journal, 1998, pp. 559-569.
— Megill, R. E. (1984), An Introduction to Risk Analysis, 2nd Edition. PennWell Publishing Co. Tulsa.
— Megill, R. E. (1992), Estimating prospect sizes, Chapter 6 in: R. Steinmetz, ed., The Business of Petroleum Exploration: AAPG Treatise of Petroleum Geology, Handbook of Petroleum Geology, pp. 63-69.
— McMaster, G. E. and Carragher, P. D. (1996), Risk Assessment and Portfolio Analysis: the Key to Exploration Success. 13th Petroleum Conference, Cairo Egypt, 1996.
— McMaster, G. E. and Carragher, P. D. (2003), Fourteen Years of Risk Assessment at Amoco and BP: A Retrospective Look at the Processes and Impact, Canadian Society of Petroleum Geologists / Canadian Society of Exploration Geophysicists 2003 Convention, Calgary Alberta, June 2-6.
— Newendorp, P. (1968). Risk analysis in drilling investment decisions. J. Petroleum Technology, Jun. pp. 579-85.
— Ofstad, K., Kittilsen, J.E., and Alexander-Marrack, P., eds. (2000), Improving the Exploration Process by Learning from the Past, Norwegian Petroleum Society (NPS) Special Publication no. 9. Elsevier, Amsterdam, 279 p.
— Otis, R. M., and Schneidermann, N. (1997), A Process for Evaluating Exploration Prospects, AAPG Bulletin v. 81, No. 7, pp 1087-1109.
— Pettingill, H.S. (2005) Delivering on Exploration through Integrated Portfolio Management: the Whole is not just the Sum of the Holes. SPE AAPG Forum, Delivering E&P Performance in the Face of Risk and Uncertainty: Best Practices and Barriers to Progress. Galveston, Texas, Feb. 20-24, 2005.
— Rose, P. R., (1987), Dealing with risk and uncertainty in exploration: how can we improve?, AAPG Bulletin, vol. 71, no. 1, pp. 1-16.
— Rose, P. R. (2000), Risk Analysis in Petroleum Exploration. American Association of Petroleum Geologists.