by Kenneth C. Hood, Guest Contributor
introduction
When geoscientists evaluate an opportunity, we tend to focus on the geological aspects we are most familiar with. This is human nature. Unfortunately, what we spend the most time on may not be the most important factor for understanding an opportunity’s potential. As an example, a team may spend many hours refining estimates of porosity or net-to-gross, when the impact of these parameters often pales in comparison to the impact of hydrocarbon column height (hydrocarbon-water contact depth).
In my assurance experience, different assessment teams have used very different representations of column height or hydrocarbon-water contact depth as part of opportunity evaluations. Often at the screening stage, they would simply evaluate an opportunity as being filled to spill. This, coupled with permissive structure sizes based on preliminary mapping of limited data, tends to result in exceptionally optimistic hydrocarbon volume estimates that almost always get reduced with additional work. Other assessors preferred an exponential decline of column heights from the assessment minimum down to synclinal spill. This would imply that every trap is almost always significantly underfilled, with essentially no chance of being filled to spill. Compared to a filled-to-spill scenario, this is a very pessimistic outlook indeed. While it is important to be as accurate as possible with column height estimates, it is also important to be consistent among opportunities, so they at least have a reliable basis for comparison.
As part of the assurance process, it is essential to verify and document assumptions about seal capacity as well as all potential geometric limits, aka leak mechanisms (including probability), and to ensure that the assessment analysis is created in a manner consistent with the geologic concept being evaluated. Experience has shown that the analyses frequently do not match the geologic description and the available constraints.
representing column height in opportunity evaluation
The details of how to best represent hydrocarbon column height in an evaluation will vary depending on software capabilities. Where possible, the workflow preferred here is to build background column heights and geometric limits (spill depth) as separate distributions. This approach enables the use of standard background column height distributions for families of related prospects while still honoring the unique configuration of each trap.
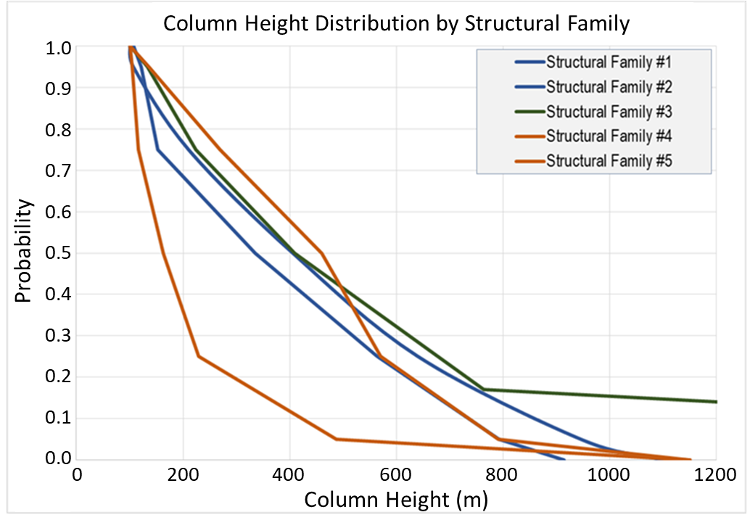
The background column height distribution is the column height supported by bed seal capacity, with a potential overprint of unresolved geometric spills (if based on analogs). Such distributions can be based on capillary constraints (e.g., capillary pressure data coupled with geologic models) or empirical column height data from local or analog discoveries (for a recent example, see Edmundson et al, 2021). Using empirical data can be challenging in that hydrocarbon pools controlled by geometric limits document the minimum column that the seal can support but not the upper limit. Figure 1 illustrates some representative background column height distributions applied to different families of structural prospects. Column height distributions should start at a consistent assessment minimum. The assessment minimum can be effectively linked to seal capacity if based on a minimum column height and not a minimum hydrocarbon volume.
The definable geometric limits on column height include controls such as synclinal spill, reservoir juxtapositions, fault intersections, and channels or scours, each with an associated probability of leak. Each probability is conditional on the success of shallower potential limits, such that the total must sum to 1.0.
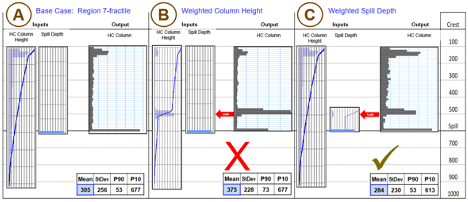
Figure 2 illustrates the importance of using separate distributions for column height and geometric limits for an opportunity evaluation. Because the input column height distribution represents the capacity of the seal to support a hydrocarbon column, in many cases it will extend beyond the trap spill(s). During the Monte Carlo convolution, both the column height distribution and the spill depth distribution are randomly sampled. The output column height for each realization is the minimum of these two values, thus creating a mode at the spill limit where the magnitude is automatically scaled to and consistent with the seal capacity. This output distribution is this displayed in a frequency format. In this example, the base case is a 600 m closure with a regional column height distribution, resulting in a mean volume of 305 MOEB (lowermost table, Figure 2A). Now consider the addition of a potential leak, such as a fault intersection, over a 50 m interval centered at 500 m below the crest. This zone has a 0.5 chance of leaking. The realizations for which this leak controls the contact should produce a mode in the output column height distribution. If this mode is represented using a weighted input column height distribution (Figure 2B), the apparent prospect volume actually increases. The increase results because the weighted input distribution reduces outcomes from above the leak as well as below it. Such behavior is not geologic – the leak should only reduce realizations deeper than the fault intersection. By using the regional column height distribution coupled with a weighted spill-depth distribution (Figure 2C), the prospect volume decreases as expected. With the weighted spill distributions, realizations above the leak are unchanged from the base case. This example illustrates how combining the background column height and explicit geometric limit(s) into a single input distribution produces non-geologic and erroneous results in Figure 2B.
Part 2 continues with a discussion of the impact of column height on opportunity evaluation. The impact on the economic viability of an opportunity can be substantial.
acknowledgements
I thank ExxonMobil for releasing this material. Many colleagues have contributed to this work.
references
Edmundson, I.S., Davies, R., Frette, L.U., Mackie, S, Kavli, E.A., Rotevatn, A., Yielding, G, and Dunbar, A., 2021, An empirical approach to estimating hydrocarbon column heights for improved predrill volume prediction in hydrocarbon exploration, AAPG Bulletin v105, n12, pp 2381-2403.
Hood, K., 2019, Hydrocarbon Column Height, Presentation at the 2019 Rose & Associates Risk Coordinators Workshop # 17, Houston, Texas.
about the author
Ken Hood holds a Ph.D. in Geology from The University of Kansas. Ken retired in 2020 after 31 years with ExxonMobil. Much of his career was spent working in assessment and assurance of conventional and unconventional resources at play and prospect scales.